Ebben a leírásban egy igazából az oldal profiljába nem vágó, de gondolkodtató feladatot írok le, amellyel a napokban találkoztam, majd adok rá egy megoldást is.
Az oldalnak nem nagyon vág a profiljába ez a leírás, talán annyiban, hogy a programozáshoz némileg köze van, mégis ajánlom elolvasni. Javaslom, hogy először a feladatkiírást értelmezve próbáld meg megoldani magad a feladatot (a megadott szabályoknak megfelelően), majd ha sikerült, vagy feladtad, nézd meg az általam írt megoldást a részletes leírással. Ha Te máshogy oldanád meg, azt kérlek írd meg egy hozzászólásba, egy darabig nekem gondolkoznom kellett rajta.
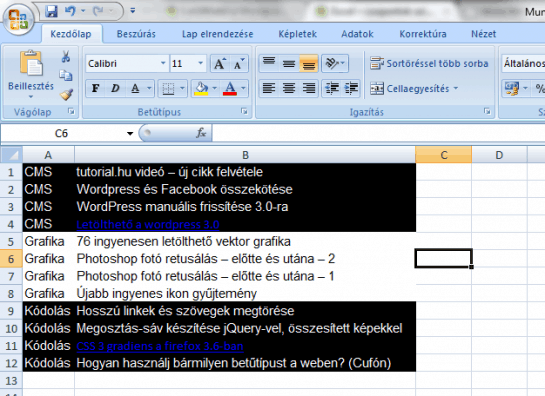
A feladat a következő: adott egy tetszőleges méretű Excel tábla, amely egyik oszlopa alapján rendezve van. Ezen oszlopban előfordulnak megegyező elemek. Például:
| CMS | tutorial.hu videó – új cikk felvétele |
| CMS | WordPress és Facebook összekötése |
| CMS | WordPress manuális frissítése 3.0-ra |
| CMS | Letölthető a WordPress 3.0 |
| Grafika | 76 ingyenesen letölthető vektor grafika |
| Grafika | Photoshop fotó retusálás – előtte és utána – 2 |
| Grafika | Photoshop fotó retusálás – előtte és utána – 1 |
| Grafika | Újabb ingyenes ikon gyűjtemény |
| Kódolás | Hosszú linkek és szövegek megtörése |
| Kódolás | Megosztás-sáv készítése jQuery-vel, összesített képekkel |
| Kódolás | CSS 3 gradiens a Firefox 3.6-ban |
| Kódolás | Hogyan használj bármilyen betűtípust a weben? (Cufón) |
A feladat: színezzük ki ezt a táblát két színnel úgy, hogy azok a sorok, amelyeknél megegyezik az első oszlop tartalma azonos színt kapjanak.
| CMS | tutorial.hu videó – új cikk felvétele |
| CMS | WordPress és Facebook összekötése |
| CMS | WordPress manuális frissítése 3.0-ra |
| CMS | Letölthető a WordPress 3.0 |
| Grafika | 76 ingyenesen letölthető vektor grafika |
| Grafika | Photoshop fotó retusálás – előtte és utána – 2 |
| Grafika | Photoshop fotó retusálás – előtte és utána – 1 |
| Grafika | Újabb ingyenes ikon gyűjtemény |
| Kódolás | Hosszú linkek és szövegek megtörése |
| Kódolás | Megosztás-sáv készítése jQuery-vel, összesített képekkel |
| Kódolás | CSS 3 gradiens a Firefox 3.6-ban |
| Kódolás | Hogyan használj bármilyen betűtípust a weben? (Cufón) |
További kikötések:
- Az Excelen belül kell maradni. Semmilyen külső eszköz nem használható
- Csak Feltételes formázás és Excel-képlet használható
A következőkben az én megoldásom szerepel, de gondolkodtató feladványról lévén szó, ajánlom, hogy először próbáld magadtól megoldani!
Alapesetben ez egy egyszerű probléma, a megoldása triviális. Tároljuk egy változóban az utolsóként használt színt, majd soronként haladva a táblázatban ellenőrizzük, hogy az aktuális sor első oszlopa megegyezik-e az előzővel, ha nem, akkor színt cserélünk. Minden sort fessünk be olyanra, amilyen szín épp a változóban van. PHP-szerű pszeudó-kódban:
<?php $color = 0; $last = array(''); /* Így inicializálunk, plusz egy feltételt megúszunk a ciklusban */ $lines = file($bemeneti_file); /* Beolvassuk a filet */ foreach($lines as &$line) { if($line[0] != $last[0]) { /* Új érték az első oszlopban */ $color = ($color == 0) ? 1 : 0; /* Színcsere */ } colorize($line, $color); /* Képzeletbeli színező függvény */ } ?> |
Csakhogy az Excel-ben nem nagyon lehet változókat és ciklust használni, és ez így túl egyszerű lenne, nincs benne kihívás. Más megoldás után kell néznünk!
Közelítsük meg más irányból a dolgot: ki tudjuk-e vajon számolni, hogy hány egyedi név fordult elő a táblában az aktuális sor fölött? Nem akarok senkit rémisztgetni az ezt a számolást végrehajtó köztes próbálkozásaimmal; a végleges megoldásomban a kulcsszó: rekurzió. Hogyan tudjuk ezt egyszerűen kiszámolni? Tegyük fel, hogy tudjuk, hogy az előző sor előtt hány egyedi érték volt. Ezután az aktuális sorra vonatkozó értéket megkaphatjuk, ha megvizsgáljuk, hogy az előző sorban levő értékkel megegyezik-e a jelenlegi sorban levő érték; ha igen, akkor ugyanannyi egyedi érték volt az aktuális sor felett, mint az előző felett, ha nem, akkor nem. Így a ciklust visszavezethetjük a rekurzió műveletre!
Egy új oszlopban (legyen a C) az első sorba vegyük fel a 0 értéket (mert ugye rekurziónál mindig kell, hogy legyen érték, aminél már nincs újabb hívás!). Utána a következő sorba szúrjuk be a =C1+HA(A1=A2;0;1) képletet, és húzzuk végig a teljes táblázaton. A rekurzív hívást láttán sokan azonnal letesznek egy-egy algoritmus használatáról, mert az úgyis lassú lesz (tévedés, algoritmustól függ, hogy mennyiszer számol feleslegesen), de ha megnézzük ebben az esetben ez O(n)-es (vagyis annyi hívás van, ahány sor), tehát nem lassabb, mint a fenti ciklust használó kódunk.
Ekkor a C oszlopban megkaptuk, hogy hány egyedi elem volt az adott sor fölött. Innen már triviális a megoldás, a változó használatát egyszerűen kikerüljük két feltételes formázási szabály használatával. Ha ugyanis egy sorban ez az érték páros, akkor az egyik színnel festjük, ha nem, akkor a másikkal (=MARADÉK(INDIREKT(‘C’&SOR();2)=0 és nem egyenlő párja).
Mi a leírás tanulsága? Azon kívül, hogy minden, egy pár perc alatt összedobható scripttel megoldható probléma kiterjeszthető fél órás gondolkodást igénylő problémává? Megfelelő módon ábrázolt adatokkal (legyen az a leírásban levő hozzáadott számérték, egy self-balancing bináris fa, akármi) sok probléma megoldható elegáns (itt: rövid, hatékony) algoritmussal.




Nekem van egy másik megoldás, ami szerintem időben hasonló lefutású, viszont látványosabban elkülönülnek a „páros és páratlan” csoportok. A megoldás hasonló, mint ami a tutorial-ban is van.
Tehát a következőt kell csinálni:
– c1-be fel kell venni a 0-t, mint kezdőértéket (ha 1-et veszünk fel, akkor mindenhol felcserélődnek a számok, tehát ezzel lehet változtatni, hogy a „páros” vagy a „páratlan” csoport legyen kiszínezve).
– c2-ben megvizsgáljuk, hogy c1 0-t tartalmaz-e.
– – Ha 0-t, akkor megnézzük, hogy a2=a1?
– – – Ha egyenlő, akkor 0-t írunk, ha nem, akkor 1-et.
– Ha c1 nem 0-t (vagyis 1-et tartalmaz), akkor megnézzük, hogy a2=a1?
– – Egyenlőség esetén 1-et írunk, különben 0-t.
Tehát maga a képlet: =HA(C1=0;HA(A2=A1;0;1);HA(A2=A1;1;0)) Ezt pedig végighúzzuk a táblázatban :)
Röviden tehát annyit csinálok, hogy ha másik csoportra váltok, akkor szimplán 0-ból 1-et (1-ből 0-t) csinálok. Ezután már egy egyszerű =0 feltételes formázási szabállyal eldönthető, hogy melyik sort kell színezni.
Tényleg… :) Így gyakorlatilag teljesen a php-szerű pszeudó-kódot kapod, csak a ciklus<->rekurzió cserével. Nekem ez a megoldás eszembe se jutott.
Bár a leírás végén levő általános érvényű igazságot (gondoljuk végig mit és hogyan tárolunk/számolunk) ezzel kevésbé tudtam volna illusztrálni. :)
BlackY
BlackY: a php-ban programozás hátrányai, hogy már az excel-t is így „programozom” :D
Egyébként ha jól emlékszem az ACM-es időkre, akkor a dupla „if” közelebb van O(n)-hez, mint a maradékos osztásos megoldásod, de egyszer majd tesztelem egy nagy táblázaton (csak ehhez visszább kellene venni a lustaságból :D).
Továbbá a fentieknél ha nem lett volna megkötés a csak excel függvény+feltételes formázás, akkor én simán makróztam volna. Kb 10-15 sornyi vbscript-el meg lehetett volna oldani az egészet segédoszlop nélkül :)
Az O(n) osztály annyit jelent, hogy az algoritmus futási idejére (legyen ez az f függvény) n-elemű (n hosszú) bemenetre igaz, hogy f(n)<=c*n+k (ahol c és k konstansok, és ennek a feltételnek csak egy tetszőleges x értéktől kezdve kell, hogy érvényesüljön). Vagyis a "közelebb van" kifejezést nem vágom :), mert mindkét algoritmus ebbe az osztályba esik. (mondjuk azt lehet mondani, hogy az f(n)=n függvényhez képest vett abszolút differencia valamelyikre kisebb, de ez meg szerintem nem a függvények távolságának definíciója) Igazából itt tényleg mérni kellene, mert itt sok minden függ az Excel beépített értelmezőjétől. Pontos adataim nincsenek, de az belülről valahogy így működhet: végigmegy az összes képleten, és felrajzol egy függőségi gráfot, amiben benne van, hogy mondjuk az A3 cellában levő képletben volt egy hivatkozás B3-ra. Utána készít egy feszítő erdőt (aminek minden fájában az összefüggő mezők vannak), a fákat a levelektől (amik már nem tartalmaznak cella-hivatkozást) kezdve elkezdi kiértékelni (esetünkben ez ugye a C1-es 0 érték lesz, utána már jöhet a C2-ben a képlet, majd a háromban etc.). Innen jön a lineáris futási idő, ha nem így működne, akkor valami nagyon exponenciális dolog jönne ki mindkét kódra, mert a fa, amit feldolgoz esetünkben egy láncolt lista lesz. A két kód közti különbség: nálam minden sorra egy összeadás, egy osztás és egy ha függvény-hívás van (3 függvény), nálad össz-vissz két ha (2 függvény). Vagyis ha ezeket a műveleteket elemi műveletnek vesszük (konstans időigény - nem), akkor 1/3-al gyorsabbnak kellene lennie a kódodnak, viszont kérdéses, hogy az aritmetikai függvények és a ha között mekkora különbség van futásban. És igen, a VBScriptes kikötés azért volt ott, hogy ne legyen egyszerű :) Az egész onnan indult, hogy kérdezték tőlem, hogy ezt hogyan lehet megoldani a legegyszerűbben, aztán abban maradtunk, hogy leginkább VBScript, de kezdett zavarni a dolog, gondoltam csak meg lehet oldani nélküle is. BlackY
Na lassan tényleg nekiesek, hogy kiderítsem, hogy MS bácsinál futásidő szerint az összeadás + osztás, vagy a „ha” a gyorsabb, mivel lényegében ennyi a különbség, ami befolyásolhatja a futásidőt :)
Egyébként az O(n)-hez közelebb dolgot csöppet rosszul írtam, mivel itt arra gondoltam, hogy kevesebb függvényhívás van egy bemeneti adatsorra, vagyis n bemeneti adatra x*n függvényhívás (tehát konkrétan arra a lehetséges 1/3-nyi futásidőbeli eltérésre gondoltam, amit ki is fejtettél, hogy elviekben hogyan jön ki).
Na de részemről a téma addig lezárva, ameddig nem csinálom meg a nagy sebességtesztet/nem találok a színezésre beépített függvényt, mert tuti, hogy van vmi csak nem tudunk róla :)
Megcsináltam a tesztet, de gyakorlatilag az excel parancsértelmezője olyan gyors, hogy egy ~950 MHz-re visszavett core2-n nincs érezhető különbség (a helyzet hasonló egy 3GHz-es HT-s Pentiumon is (Prescott mag :D)). Lényegében 2 másodperc alatt újraszámolja a teljes táblázatot (1048576 sor, vagyis a 2007-es excel maximális munkalap mérete), valamint a színezést is megcsinálja.
Ha valakit esetleg érdekel a táblázat, akkor itt egy link, ahonnan letölthető (A-tól C-ig az én módszerem, G-től I-ig BlackY-é):
http://data.hu/get/2762093/tutorial_hu_excel_sebesseg.xlsx (~40MB)
A C1-ben, illetve I1-ben levő szám megváltoztatása (0-ra vagy 1-re) újraszámoltatja a teljes táblázatot, ami megmutatja, hogy melyik a gyorsabb. Akinek esetleg van egy lassabb gépe sok rammal, azt leírhatná, hogy melyik módszer a gyorsabb :)
=HA(A2=A1;C1;NEM(C1))
Szerintem ez egyszerűbb képlet és talán kicsivel gyorsabb is.
Egy segédoszlop felvétele néha egyszerűbb mint makrót írni, főleg ha a makrók betöltése tiltva van.